Cómo saber la hora mirando las estrellas

(Hace unos 20 años conseguí que me publicaran un artículo en una revista nacional de astronomía. En efecto, durante los meses de septiembre y octubre de 1997, la revista Tribuna de Astronomía, del grupo Sirius, publicó un artículo que describe cómo cualquier noche del año es posible saber la hora mirando el cielo nocturno y haciendo unos sencillos cálculos mentales. 20 años después, al revisarlo, yo cambiaría algunas expresiones y haría otros gráficos, pero he preferido mostrarlo tal como lo publicaron, incluyendo los gráficos 'vintage'.)

Cómo Saber la Hora mirando las estrellas

Revista nacional "Tribuna de Astronomía"

Septiembre y Octubre de 1997

Fue la belleza del cielo nocturno lo que siempre me llamó más la atención, si bien tras muchos años de observaciones mi forma de considerar la gran bóveda celeste ha cambiado. Al principio de todo, cuando no conocía figuras o nombres, ni tan siquiera a Orión, era fascinante perderse (y nunca mejor dicho) en ese cielo en desorden salpicado de multitud de puntos azules, blancos, amarillos,  anaranjados y rojizos. Una vez que pasó el tiempo mirar al cielo resultó mas sencillo y dramático; por donde quiera que lo hacía no dejaban de aparecer figuras y personajes mitológicos, nombres de héroes y recuerdos de sus gestas lejanas. El cielo, para mí, perdió entonces el encanto de lo desconocido, de lo profano, para no dejar de ser un campo de continuos descubrimientos sobre las reglas que regían ya no el desorden sino la armonía. Ahora, a veces pienso que tristemente, es todo mucho más racional, y la experiencia, unida al conocimiento, me ha dejado una serie de trucos que extraer a la noche. Uno de ellos es mirar a las estrellas y con un margen de error no mayor a diez, quince minutos (a veces incluso el exacto), saber la hora que es sin mirar el reloj, lo que por cierto no es nada complicado, tan sólo hay que saber dónde está la constelación de la OSA MENOR y seguir ciertas reglas muy sencillas. Por supuesto, que nadie espere conocerla con la precisión que alcanza un reloj; según afinemos nos moveremos en un principio en errores que oscilarán entre 0 y 30 min., que con la experiencia iremos afinando hasta esos diez minutos. El método a seguir lo componen varias ideas muy sencillas que voy a repetir una y otra vez (para que todo quede claro). Dicho esto, abordemos el problema.

Preliminares

1- Para saber la hora mirando las estrellas nos ayudaremos de la OSA MENOR, que desde Europa y

norte de Africa es una constelación que se ve cualquier noche del año a cualquier hora (esto se debe a que es circumpolar, o que no desaparece nunca bajo el horizonte).

La estrella más brillante de la Osa Menor es la ESTRELLA POLAR, que además de señalar al norte

geográfico (es la única estrella "fija" en el firmamento) posee la curiosa propiedad de que todas las estrellas del cielo "dan una vuelta" alrededor suya en aproximadamente 23h56m (un día sidéreo). Así, al cabo de 24h (un día oficial) una estrella ocupa la misma posición que ocupaba el día anterior a esa misma hora, más esos 4m de arco de giro (a esta diferencia de aproximadamente 4 minutos existente entre el día oficial y sidéreo se le llama aceleración de las fijas).

2- Esto es, si consideramos el cielo como un gigantesco reloj rígido que da una vuelta en un día oficial, cuyas posibles manecillas son los segmentos que unen cualquier estrella con la polar, se trata de un reloj que adelanta 4m al día, o 1h a los 15 días, o 2h a los 30 días, o 2h4m a los 31, etc. Así, si una estrella ocupaba cierta posición el día 4 de Junio a las 3 de la madrugada, por ejemplo, ocupará esa misma posición el día 5 de Junio a las 2h56m de la mañana, el día 6 de Junio a las 2h52m de la madrugada, el 19 de Junio (15 días después del primer día) a las 2h de la madrugada, el 4 de Julio (30 días después) a las 1h de la madrugada, el 19 de Julio a las 12 de la noche, el 21 de Julio a las 23h52m... y la ocupó el 3 de Junio a las 3h4m, el 1 de Junio a las 3h12m, el 31 de Mayo a las 3h16m, el 1 de Mayo a las 5h16m... Esto es, se trata de un reloj que adelanta 4m por día, luego si desde una noche determinada deseamos ir hacia el futuro, hemos de quitar 4m por día que transcurra, y si vamos hacia el pasado los hemos de sumar. Por cierto, el movimiento de las estrellas alrededor de la polar se realiza en sentido contrario al de los relojes ordinarios.

3- Como en el procedimiento que vamos a seguir hemos de pasar de unas fechas a otras, de no realizar todos los cálculos en hora astronómica tendríamos que tener en cuenta si tales fechas consideradas, así como la de partida, lo son de horario de verano o de invierno, y estaríamos continuamente sumando o restando horas de ajuste en cada paso. Lo más sencillo es realizar todos los cálculos en hora astronómica, y por ello, todas las cifras que se van a suministrar están expresadas en tiempo universal, y sobre ese tiempo, independientemente del horario de verano o invierno o de donde nos encontremos, efectuaremos los cálculos. Cuando hayamos terminado de calcular y podamos decir "es tal hora astronómica" pasaremos a la hora oficial del país en cuestión, sumando o restando las horas que separen a ésta de la astronómica en dicho lugar. En la España peninsular sumaríamos al resultado en U.T. una o dos horas según estuviésemos en el horario de invierno o de verano, una o ninguna en Canarias, respectivamente (cada año se realiza el proceso de adelantar o retrasar los relojes una hora oficial en fechas distintas, aunque como indicación, los cambios de horas se suelen producir en Europa los meses de Marzo-Abril y Setiembre-Octubre, por lo que los meses de Mayo, Junio, Julio y Agosto suelen tener el horario de Verano, y Noviembre, Diciembre, Enero, Febrero el de invierno. Habría que tener cuidado en Marzo, Abril, y Septiembre, Octubre. Marruecos no cambia la hora, y está permanentemente en U.T.).

4-  Como decía, se puede considerar el cielo como un gigantesco reloj que cada día da una vuelta alrededor de la polar en 23h56m. Como se trata de un reloj rígido (las estrellas no se mueven entre sí de una noche para otra), es suficiente definir una sola manecilla del mismo (al igual que ocurre con los relojes despertadores analógicos; una manecilla es suficiente para señalar la hora a la que  queremos que suene el timbre, estando ésta normalmente cuantizada en tramos de 10m). Elegiremos como manecilla y la llamaremos PUNTERO-A, o bien PUNTERO, al segmento que une la estrella polar con Kochab (beta UrsaMinoris, la segunda estrella más brillante de la Osa menor), tal que este puntero va a dar una vuelta al cielo en sentido contrario al de los relojes usuales en las citadas 23h56m. Véase la Fig.1.

Como nuestras manecillas de reloj, que son todo el cielo, se van a superponer a una graduación imaginaria fija que ha de representar las 24h del día oficial (hay que leer las horas en alguna parte), y como el cielo posee una amplitud angular de 360º (sobre éste se dibuja la graduación imaginaria fija), nos damos cuenta de que cada 15º del reloj móvil han de representar una hora (360º/24hora=15º/h), cada 7'5º media hora... para no provocar ningún tipo de discordancia. Esto es, acabamos de graduar el reloj.

5- Consideremos el reloj, cuyo representante es la manecilla puntero. Todo el reloj y el puntero se desplazan sobre una graduación imaginaria fija similar a la de los relojes ordinarios, pero como este reloj del cielo es tan peculiar que da una vuelta apróx. cada 24h y en sentido contrario, la graduación es la que representa la Fig.2 (en la que por cierto el puntero señala las 17h00m).

Nótese que esta graduación carece de ambigüedad, pues la estrella polar no se encuentra en el zenith del observador (el punto superior de la bóveda celeste), sino a cierta altura sobre el horizonte en determinada dirección (norte), por lo que mirando dicha estrella es posible definir las direcciones "encima de ella" (0h), "debajo de ella" (12h o norte geográfico), "a la izquierda" y a la "derecha de ella" (6h y 18h respect.) Véase la fig.3. A partir de ahora, y contrariamente a la notación usada en la citada figura 2, voy a designar por el par (H,M) a las Horas y Minutos de la graduación imaginaria fija, y por la terna (h,m,s) a las horas, minutos y segundos del tiempo cotidiano, siempre en U.T.

6- Atención, pues esto es ya importante, vamos a dar un dato inicial; la hora exacta de cierta noche en la que el puntero está en una posición determinada (la vertical superior). A las 0h0m de la madrugada de la noche del 11 al 12 de Mayo, el puntero señala las 0H0M. Por ello, a las 6h00m señalará las 6H, a las 12h00m las 12H, a las 18h00m las 18H de la graduación, y caso de no darse aceleración de las fijas, señalaría de nuevo las 0H a las 0h00m de la madrugada del 12 al 13 de Mayo, pero por la citada aceleración de apróx. 4m, a las 0h00m señalará las 0H4M. Conviene no confundir el reloj móvil (todas las estrellas del cielo, incluido el representante puntero) con la graduación imaginaria fija. El origen de esta dualidad es que los relojes ordinarios no atrasan o adelantan 4m cada jornada, sino que de un día para otro la hora es esencialmente la misma, y basta con superponer las manecillas a la graduación (esto es, mirar el reloj) para saber qué es. En el gran reloj celeste no ocurre así; de un día para otro se va produciendo cierto desfase, y para conocer la hora real hay que conocer cuantos días han pasado desde determinada fecha inicial (así, a razón de 4m diarios, conoceríamos la  desviación total sufrida), y a qué hora (h,m) estaba la manecilla en determinada posición (H,M) el día

original.

7-  El proceso a utilizar es muy sencillo y mecánico, y con todo lo que se ha dicho hasta aquí ya somos capaces de saber la hora por las estrellas. Lo que vamos a hacer a partir de ahora no es sino volver sobre las ideas anteriores, repitiéndolas una y otra vez al detallar el método y considerar los ejemplos. Al final, en los APENDICES 1 y 2 aclararemos cómo mejorar la precisión. Dicho esto, vayamos al grano.

El método en sí

El proceso de conocer la hora lo componen dos etapas; la asignación de ángulo y el cómputo de días.  

Asignación de ángulo. 

La ASIGNACION DE ANGULO es la parte no mecánica y más delicada del proceso, pues al ser puramente visual, se suele cometer la mayor parte del error. Mirando al cielo y viendo la posición del puntero, y considerando la graduación imaginaria fija de amplitud 24h de la Fig.2, hay que conocer qué hora señala el mismo. Sin ninguna dificultad veremos si el puntero está en el primer cuadrante (de 0 a 6H), en el segundo (de 6 a 12H), etc. incluso en qué octante está, de donde sabemos que como mucho cometeríamos un error de 3h. Pero lógicamente deseamos una precisión mayor ¿qué hacer? cuando el puntero está muy cerca de las 0, 6, 12 o 18H es fácil, pues está en posición casi vertical o casi horizontal, pero cuando no sea así convendría conocer otras posibles manecillas, y la distancia, en ángulos o en tiempo, que las separa del puntero-A, pues posiblemente alguna de éstas sí pase cerca de los ejes imaginarios de la graduación, facilitando la identificación. Además de que si conocemos los ángulos que forman dos manecillas determinadas es más sencillo medir otros ángulos en el cielo.

Y para eso añado la Fig.4, donde además del puntero-A, consideramos la manecilla B que une Polaris con Pherkad, también de la osa menor, las manecillas C y D, que unen polaris con ciertas estrellas de la constelación de Dragón en clara formación triangular isoscélica (desgraciadamente estas estrellas no se ven desde las ciudades), y la manecilla E, que une Polaris con Alfirk (beta Cephei), que es casi perpendicular al puntero A, esto es, el paso de A y E por un punto dado dista aproximadamente 6h o 90º. Para visualizar bien las distancias entre los punteros A, B, C, D, E, véase la comentada Fig.4. 

Para una primera aproximación es suficiente la citada figura que representa todo un cuadrante móvil.

Cómputo de días.

Qué es el COMPUTO DE DIAS? Sabemos cuánto adelanta el reloj de una noche para otra (4m), luego por un proceso de repetición, y partiendo de que el puntero señala las 0H de la graduación fija la noche del 11 al 12 de Mayo a las 0h00m (o el puntero-B las 0H a las 0h30m, o el puntero-D las 6H a las 9h30m etc. Elíjase y apréndase un paso determinado un día determinado, yo recomiendo usar el puntero-A porque es el más brillante); elegida una determinada noche podemos saber el momento (a razón de sumar/restar 4m cada día que falte/transcurrido hasta/sobre el 12 de Mayo) en que el mismo señalaba las 0H en la noche de observación, y conociendo la asignación de ángulo conoceríamos cuánto tiempo habría pasado desde entonces, por lo que haciendo una sencilla suma sabríamos la hora astronómica. Sumando, en España, 1 ó 2h según corresponda obtendríamos la hora buscada, con lo que finalizaría el proceso. En esta etapa no se suelen cometer errores, son todos cálculos mecánicos.

         

NOTA IMPORTANTE: Como ya había dicho, el puntero pasa por la vertical superior la noche del 12 de mayo a las 0h00m, por lo que suponiendo que el año siguiente no sea bisiesto también realizará ese mismo tránsito los días:

¿Cómo es esto posible? Esto es, se supone que al cabo de un año los valores deberían coincidir, y nada de eso, tras ese tiempo hemos adelantado 20m, de donde de un año para otro no nos valdrían todas las fechas que conocemos ¿por qué? Es muy simple; volviendo al punto segundo y a la diferencia entre los días sidéreo y oficial, yo decía que la aceleración de las fijas es de aproximadamente 4m, y por no tomar la cantidad exacta se comete cierto error diario que se va acumulando, tal que al cabo de un año se ha convertido en la nada despreciable cantidad de 20m.

Esto se puede subsanar en parte si para calcular la posición de marzo, por ejemplo, partiendo desde el 12 de Mayo, no hacemos lo que se llama la vuelta tonta y pasamos por Junio, Julio, Agosto, Septiembre, Octubre... sino que buscamos Marzo por el camino más corto, que es ir hacia atrás en el calendario (Mayo, Abril y Marzo). De otro modo; 4m es una aproximación, y cuantos más días pasen, el error acumulado será mayor, luego si nos interesa pasar de una fecha a otra conviene hacerlo del modo que menos días sumen. Así, para calcular posiciones de Abril, Marzo, Febrero, Enero, Diciembre y Noviembre es mejor ir hacia atrás en el cómputo de días, y para Junio, Julio, Agosto, Septiembre y Octubre es mejor ir hacia delante, por lo que cometeríamos un error máximo de 10m en el cómputo de días, que no es mala aproximación para aquellos que no quieran realizar muchas operaciones mentales.

Sigamos; a pesar de cometer una imprecisión aditiva en el cómputo de días, pudiera ser que el error que cometamos en la asignación de ángulo se compense con este acumulado, resultando la hora

exacta, pero cabría también la posibilidad de que ambos errores se sumasen, alejándonos más de la hora buscada. Lo más adecuado parece, sin lugar a dudas, conocer exactamente cuál es la aceleración de las fijas, y no conformarnos con el valor de 4m. Una nueva y mejor aproximación es tomar una aceleración de 3m57s (en el Apéndice 1 optimizo aún más esta magnitud). Esta aproximación de 3m57s es para mí suficiente, tal que evitando realizar la vuelta tonta, el error acumulado sería de menos de 1 minuto cada 6meses. La ventaja de considerar los 3m57s/día es que para corregir el desfase que producían los 4m/día, las unidades aún son sencillas, la corrección (sobre los 4m/día, 1h/15d, 2h/30d...) es de 15seg a los 5 días, 30seg a los 10d, 1 minuto cada 20 días... Así, la tabla de tránsitos del puntero por las 0h de la graduación es aproximadamente:

Ejemplos Comentados

Antes de entrar en los diagramas, quiero aclarar varios puntos acerca de los ejemplos que vamos a ver. 

• Para simplificar los cálculos, no en vano estamos empezando y es lógico que si deseamos obtener mayor precisión debamos efectuar operaciones más complicadas (la Naturaleza suele comportarse así), todos los cómputos de días de los ejemplos que siguen se van a hacer para una aceleración de las fijas de 4m, partiendo de un puntero el 12 de Mayo, y no efectuando la vuelta tonta. Para empezar a practicar es mejor hacerlo así; el posible error que podemos cometer es de magnitud, no de método; éste es esencialmente correcto. Profundizando en esto, partiendo del 12 de Mayo y de una aceleración de 4m, el 10-11 de Noviembre se produciría el máximo error; según fuésemos hacia atrás o hacia delante obtendríamos los valores 12h08m o 11m52m respect. (el tránsito exacto es 12h00m, el opuesto a la posición de partida), así que desde el 12 de Mayo hasta el 10 de Nov. deberíamos ir hacia delante, del 11 de Nov. al 11 de Mayo hacia atrás); al no dar la vuelta tonta nunca cometeremos un error mayor de 10m (sería superior a los 5m en los meses más alejados de Mayo; Septiembre, Octubre, Noviembre, Diciembre, Enero). Una vez que se tenga soltura en el proceso y se comprenda mucho mejor, tómese la aceleración de las fijas de 3m57s, y no más, no merece la pena afinar errores inferiores a un minuto, margen de error del método.
• Cuando digamos que es una noche determinada, entendemos que en esa misma fecha se produce el amanecer. 
• Todos los razonamientos que siguen parten del 12 de Mayo a las 0h00m. Esto no es imprescindible; se puede partir de cualquier fecha y en la última columna ya suministré otros tránsitos posibles, o elíjase el 3 de Julio que tiene la particularidad de ser el "día central del año", por lo que en el cómputo de días para ir hasta el 1 de Enero se suma, y hasta el 31 de diciembre se resta, o alguna fecha que recuerde fácilmente (algún cumpleaños o aniversario). Pero por favor, NO se aprenda los pasos de todos los punteros los 365 días del año (esto, obviamente, sería el caso más extremo y desaconsejable), sino los de una sola fecha y un sólo puntero, y parta siempre de ahí (todas las fechas se deducen de una sola al conocerse perfectamente el retraso diario). Se ahorra en memoria y se gana en seguridad.
• Si en algún momento del cómputo de días hay que pasar por los últimos días de Febrero, según sea bisiesto o no dicho año, lo consideraremos como de 29 ó 28 días respectiv. Para los ejemplos que vienen asumo que el año de observación no es bisiesto. 

Dicho esto, vayamos con los citados ejemplos ordenados según dificultad creciente.

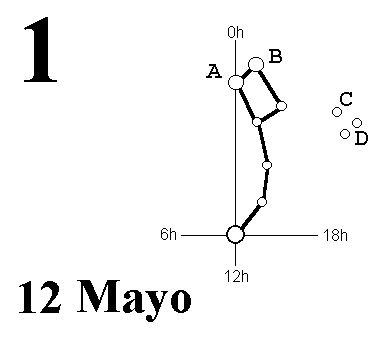
1. No hay mucho que comentar, estamos a 12 de Mayo y el puntero señala las 0H0M, (esto es, es la posición de partida, la única que realmente tengo aprendida) luego son las 0h0m U.T. Como con toda claridad el 12 de Mayo "pertenece" al horario de verano, si estamos en la península sumamos dos horas y obtenemos la hora oficial, esto es, nuestros relojes de muñeca han de marcar las 2h de la madrugada.

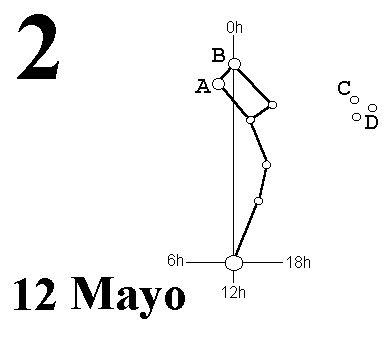
2. El puntero-A se ha desplazado media hora respecto la posición anterior, pues el puntero-B que viene 1/2h detrás, señala las 0H. Como el 12 de Mayo se produce el tránsito del puntero por las 0H a las 0h0m, y ha pasado 1/2h desde entonces, son las 0h30m de la madrugada, hora astronómica o U.T.

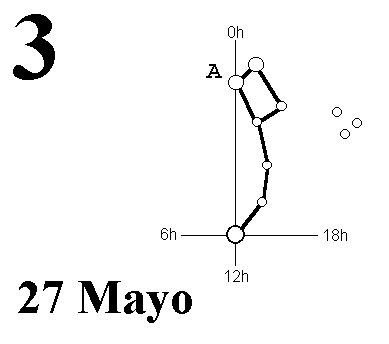
3. De estar a 12 de Mayo, como el puntero señala las 0H0M, serían las 0h0m, tal como hemos visto, sin embargo no estamos en esa fecha, sino que han pasado 15 días desde entonces. Como 15 días hacia el futuro se corresponden a 1h de adelanto (cómputo de días), el 27 de Mayo se realiza el tránsito por las 0H a las 0h0m-1h=23h0m, hora astronómica. Al igual que los dos ejemplos anteriores, si estamos en la península le podemos sumar dos horas para pasar a la oficial; en canarias, tan sólo una.

4. Desde el 12 de Mayo hasta el 12 de Junio han pasado 19+12=31 días, que a razón de 4m por día suponen un adelanto de 31x4m=2h04m. Esto es, el puntero estuvo en posición vertical a las 0h0m-2h04m=21h56m. Sé que la estrella o puntero C está sobre la vertical; entonces, como la diferencia entre A y C es de 2h50m, habría pasado ese tiempo desde que el puntero estuvo en posición vertical. Luego son las 21h56m+2h50m=0h46m U.T.

5. Van complicándose los diagramas, y ya no dibujo tantas líneas. Por el cómputo de días han pasado 19+30+31+31+30+20=161 días desde el 12 de Mayo, que a razón de 4 min cada día serían 10h44m, luego el puntero estuvo señalando las 0H a las 13h16m. ¿Cuánto tiempo ha pasado desde que estuvo allí? Al menos 6h, pues está en el segundo cuadrante, pero hay que afinar más. Como C y D están separadas unos 40m, y parece ser que la separación entre C y la línea de las 6H es idéntica a la de C y D; C estaría indicando las 5H20M, luego el puntero, que se separa 2h50m de C, no puede sino indicar las 5H20M+2H50M=8H10M, recorriendo ese tiempo desde que estuvo en posición vertical. Luego son las 13h16m+8h10m, esto es 21h26m U.T.

6. El cómputo de días me dice, si no doy la vuelta tonta, que debo restar 11+30+31+23d, luego para conocer en qué momento estuvo el puntero arriba efectúo 0h0m+95x4m=6h20m. Ahora viene la difícil asignación de ángulo. Parece ser que el ángulo entre C y D es una vez y media el que separa D de la línea de las 12h, o el que separa a A y B es la tercera parte del que separa a A y la línea de las 18H. Como AB=30m, a A le faltan 1h30m para llegar a las 18h. Luego el puntero señala las 16H30M, y claro, tras sumar a 6h20m son las 22h50m U.T.

7. El ejemplo más difícil y el que en realidad nos encontraremos, pues en el cielo no hay líneas ni ángulos de ninguna clase, sino estrellas. Quiero aprovechar para enseñar, cuando tomamos una aceleración de las fijas de 4m, un modo más cómodo de efectuar el cómputo de días, que no es sino ir sumando o restando 2h por cada mes que pase (en un principio consideramos los meses de 30 días) desde Mayo hasta el deseado, sumar o restar días hasta llegar a la fecha deseada, y ajustar los días que podemos haber suprimido o suministrado (contamos los meses como de 30 días pero algunos poseen 28-29 ó 31). El resultado final es el mismo, pero simplifica las operaciones mentales. Bien, para ir de Mayo a Enero hemos de ir hacia atrás; el 12 de Mayo a las 0h0m, el 12 de Abril a las 2h0m, el 12 de Marzo a las 4h0m (y nos hemos comido un día, pues Marzo tiene 31), el 12 de Febrero a las 6h0m (aquí suministramos dos, pues Febrero tiene 28 y no 30), y el 12 de Enero a las 8h0m, comiéndonos otro día. Del 12 al 1 hemos de sumar (vamos hacia atrás) 10 días más, luego tránsito del puntero a las 8h40m. Queda por ajustar si los meses tenían 28 o 31 días. Nos hemos comido dos días en el 31 de Enero y 31 de Marzo, y hemos añadido dos con el 29 y 30 de Febrero, esto es, en este caso no hay que ajustar nada (si no se sumarían o restarían 4m por cada día que hubiésemos afectado según fuésemos hacia atrás o hacia delante. La otra opción, que requiere hacer más operaciones mentales, es sumarle a 0h0m (10+30+31+28+31)x4m, vuelve a salir que el puntero estuvo arriba a las 8h40m, y señalará las 12H a las 20h40m. ¿Cuanto le falta? El truco es percatarse de que la separación entre D y la línea de las 6H es dos veces y media el ángulo CD (40m), luego D pasó hace 1h40m por las 6H. Luego a A le falta 50m para llegar a las 12H, luego son las 20h40m-50m=19h50m U.T.

Antes de ir con el último ejemplo (resuelto tanto con una aceleración de 4m como de 3m57s), deseo practicar el cómputo de días. Para ello voy a cambiar las supuestas noches de observación, indicando, a modo de comprobación, en qué momento se produce el paso del puntero por la vertical, siempre en U.T. Por cierto que algunas horas resultan ser pleno día, y es que el procedimiento que se ha enseñado es válido para cualquier momento, día o noche (por circumpolaridad) siempre que se vea el cielo, claro.

8A. ACELERACION DE 4m; Claramente la asignación de ángulo me dice, puesto que A y E están separadas 6h40m, y E señala las 6H, que el puntero señala las 12H40M. Veamos el cómputo de días mediante el modo "pocas operaciones mentales". 12 de Mayo 0h, 12 de Abril 2h, 12 de Marzo 4h (me como un día), y del 12 de Marzo al 29 de Febrero (último día de mes) 11 días a sumar, luego 4h44m. Como me he comido el 31 de Marzo, el paso del puntero se produjo a las 4h48m. Luego son las 12h40m+4h48m=17h28m U.T. 

8B. ACELERACION DE 3m57s; La asignación de ángulo no varía y el puntero sigue señalando las 12H40M, la pregunta es saber qué tiempo lleva acumulado el nuevo cómputo de días. Cuando se toma esta aceleración lo más conveniente es realizar el cómputo de días hallando el número total de días, en este caso 11+31+30=72d, que a razón de 4m/día son 4h48m, pero a esa cantidad hemos de quitar 3s/día o 1m/20d. En total hemos de quitar 3m36s, aproximadamente 4m. Como vamos hacia atrás, si esas 4h48m se suman, estos 4m se restan (si vamos hacia delante, todo lo contrario), y el tránsito del puntero se produjo a las 0h0m+4h48m-4m=4h44m, a sumar a las 12h40m, resultando una hora más precisa (no mucho más), de 17h44m. Tomar una aceleración más exacta creo que no merece la pena.

Conclusiones

Aunque la explicación parece larga y compleja, todo es bastante sencillo y se resume en varias ideas, que se han repetido una y otra vez, y de las cuales puede deducirse todo lo demás. Esas ideas, esos datos que sí hay que aprender son:

1. Todos los cálculos se deberían hacer en hora astronómica, para una vez finalizado el proceso, pasar a la hora oficial.
2. El firmamento da una vuelta alrededor de la polar en apróx. 23h56m, esto es, el reloj adelanta aproximadamente 4m por día; esto es, sumamos 4m por cada día que vayamos hacia atrás, los restamos por cada día que vayamos hacia delante. Ojo al 10-11 de Noviembre. Si se quiere más precisión, elíjase un adelanto de 3m57s. En todo caso, es conveniente no dar la "vuelta tonta". Al cabo de un año estos errores se han compensado.
3. Dicho giro continuo se realiza en dirección contraria a la de las agujas del reloj.
4. El 12 de Mayo a las 0h00m U.T. el puntero señala las 0H.

Y el resto, como decía, es totalmente deducible de las cuatro reglas anteriores. Buena suerte.

APÉNDICES

Apéndice 1

Tomar una aceleración de las fijas de 4m no es mala idea, pero puede inducir un error notable, especialmente si damos la vuelta tonta. Dicho error es prácticamente despreciable si tomamos una aceleración de 3m57s, que es lo que yo recomiendo. Ahora bien... ¿cuánto se separan esos 3m57s del valor exacto de la aceleración? ¿de verdad que no merece la pena afinar tanto y es suficiente tomar 3m57s? No es difícil responder a estas preguntas, pues al cabo de un año exacto (tomo A=365'242199días como aproximación del año trópico, o el tiempo que le lleva a la Tierra dar

una vuelta alrededor del sol), incluyendo bisiestos, las estrellas vuelven a sus mismas posiciones, luego o bien no se comete desfase de un día para otro (cosa que no sucede pues ya hemos visto que se produce cierto adelanto), o bien este desfase es de múltiplos exactos de un día o k/A años cada día (en concreto k=1 pues 365x4m es aproximadamente un día), para que al cabo de un año de A días, este error se compense, apareciendo las mismas posiciones estelares en las mismas fechas. Como los decimales no son del todo exactos aún cometeríamos ciertos errores (en el truncamiento de los decimales se encuentran implícitos errores mínimos no subsanables como porqué y como se toman los años bisiestos, además de que no quiero entrar en disquisiciones acerca del tiempo sidéreo o la precesión de los equinocios, de consecuencias insignificantes en el método y que añadirían mucha dificultad al problema), pero estos ya serían errores insignificantes. Como decía, la aceleración diaria es, aprox., 1/A años = 236'55seg = 3m56'55seg, que es ya una buena aproximación de la aceleración de las fijas. Nótese que el desfase con los 4m es de 3'45seg, que al cabo de 365'25 días se convierte en ­21m! (tomando la aceleración 4m nos desviábamos hasta 20m). Por lo que al considerar esa aceleración de las fijas de 3m56'55s, independientemente de la vuelta tonta, cometeríamos un error en el cómputo de días no superior a 1 minuto (21-20), que es una cantidad demasiado aceptable. Así, conociendo esto, el único error que podríamos cometer es el de la asignación de ángulo, donde no hay demasiadas reglas salvo atinar con la vista. Quedaría un pequeño detalle, dar unas unidades más adecuadas que esos 3m56'55s por día y eso es muy delicado, al no tener múltiplos cómodos. De hecho, no dejo de repetirme en que es suficiente considerar la aceleración de las fijas como de 3m57seg, con lo que cometería un error máximo de 0'45seg/día, o de menos de 2m al año aún dando la vuelta tonta. Tomando 3m56'55s podemos conocer el computo de días al segundo, lo que va a necesitar de operaciones mentales más complicadas, y que no va a tener mucho sentido cuando en la asignación de ángulo vamos a cometer errores de varios minutos.

Apéndice 2

Sigo en mi intención de explicar los errores, mínimos, cometidos al detallar el método. En esta sección voy a expresar, con un margen de error de un segundo, las diferencias entre punteros, comparándolas con las separaciones que había tomado. Para obtener dichas aproximaciones óptimas me baso en la ascensión recta (A.R.) de tales estrellas, o el tiempo transcurrido desde que el punto vernal cruzó el meridiano del observador, por lo que puedo conocer, efectuando sencillas sustracciones, el tiempo entre los diversos punteros. 

A.R. PUNTERO-A (Kochab)  14:50:43

A.R. PUNTERO-B (Pherkad) 15:20:44

A.R. PUNTERO-C (Psi-Dra) 17:42:01

A.R. PUNTERO-D (Chi-Dra) 18:21:08

A.R. PUNTERO-E (Alfirk)  21:28:37

Así, efectuando sencillas restas, las diferencias son:

ENTRE A y B;  0h30m01s ; (yo había tomado 30m)

ENTRE B y C; 2h21m17s ; (yo había tomado 2h20m)

ENTRE C y D; 0h39m07s; (yo había tomado 40m)

ENTRE D y E; 3h07m29s; (yo había tomado 3h10m)

Se aprecia que las aproximaciones, aunque afinables (podemos cometer un error de hasta 2m30s en el caso D-E), no son malas, y al tomarse en múltiplos de 10m facilitan su memorización. Por supuesto, para quien quiera afinar más, aquí están las cifras exactas aunque pienso que no merece la pena ajustar tanto.

Para completar este apéndice, doy las ascensiones rectas de otras estrellas notables en las inmediaciones de la polar, así como un mapa en el que localizarlas, por si se desean usar como nuevos punteros.

A.R gamma Camelopardalis 03:49:59

A.R alpha UrsaMayoris (Dubhe) 11:03:31

A.R gamma Cephei (Er Rai)  23:39:12

Texto y Gráficos: Gonzalo Pedrera Quintana